東京理科大学理学部第一部数学科 | カリキュラム | 東京理科大学 理学部第一部数学科

代数学は数や方程式の理論から始まりました。2次方程式の解の公式は中学校で学びますが、3次、4次方程式にも解の公式があります。しかし、5次以上の方程式には解の公式が存在しないことが知られています。その証明を導く過程から、現代の代数学で基本的な言語ともいえる群論、環論、体論が生まれてきました。現代代数学では、これら群論、環論、体論を基本とし、さらに新しい数学的道具を発明・開発することで、最先端の理論が研究され発展しています。私たちの学科では、整数論、有限群の表現論、多元環の表現論の研究をしています。

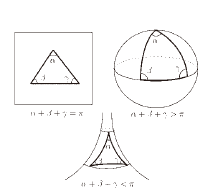
幾何学とは、ある変換群が作用する空間内の図形の性質でその変換群に属する各変換によって不変なものを調べる学問です。変換群が作用する空間を一つ選べば、その空間内で一つの幾何学が展開できるわけです。最もスタンダードな幾何学は、ユークリッド幾何学とよばれる曲率0のユークリッド平面(あるいは、空間)上の幾何学です。
高校で教わる幾何学はユークリッド幾何学です。その他、正の曲率をもつ球面上の幾何学、負の曲率をもつ双曲平面上の幾何学が基本的です。アインシュタインの相対性理論で取り扱われる時空の研究は、ローレンツ幾何学とよばれる幾何学の研究に相当し、幾何学は、物理学とも深い関わりをもっています。

解析学は、高校の数学Ⅱや数学Ⅲで学ぶ微分積分から始まる学問分野です。本学科では、より発展的な微分積分を学んだ後、解析系の講義として、複素関数論、微分方程式、ルベーグ積分、関数解析を学びます。解析学は、それ自身、数学の１分野であり数学として興味深い話題がたくさんある一方で、ニュートンの力学に起源をもち、歴史的に物理とのつながりがあります。現在では、理学および工学の幅広い分野に解析学が用いられており、純粋に数学を志す人ばかりでなく、数学の応用を志す人にも向いています。

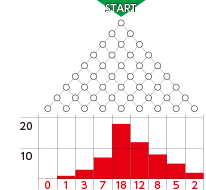
一見無秩序な現象でも、何度も起こると規則性が現れることがあり、これは調査や予測に生かせます。またブラウン運動のように無秩序な力が絶えず加わる運動は、方程式から法則性を解明できます。数理ファイナンスさらにはデータサイエンスなど、ランダムな現象を把握するための理論の適用範囲は広がりつつあります。

数学教育とは数学の教え方を学ぶものと思われがちです。もちろん教え方も扱いますが、その教え方を生み出す原理まで明らかにします。すなわち、数学教育学とは、教科内容の本質を追求し、学習や指導の原理を明らかにする学問といえるでしょう。数学教育の研究室では、中学・高校で学んできた数学を「教える立場」から追究し深く理解し直します。そして、数学の深い理解に基づいて、生徒の思考力や創造性を育成する教材、指導法・評価法、カリキュラムの開発を行います。また、実験授業や調査を通してそれらの有効性や実践可能性を科学的に究明します。